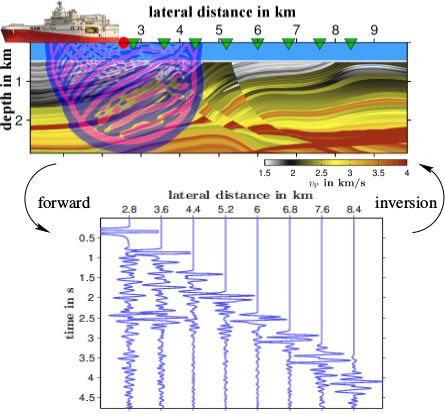
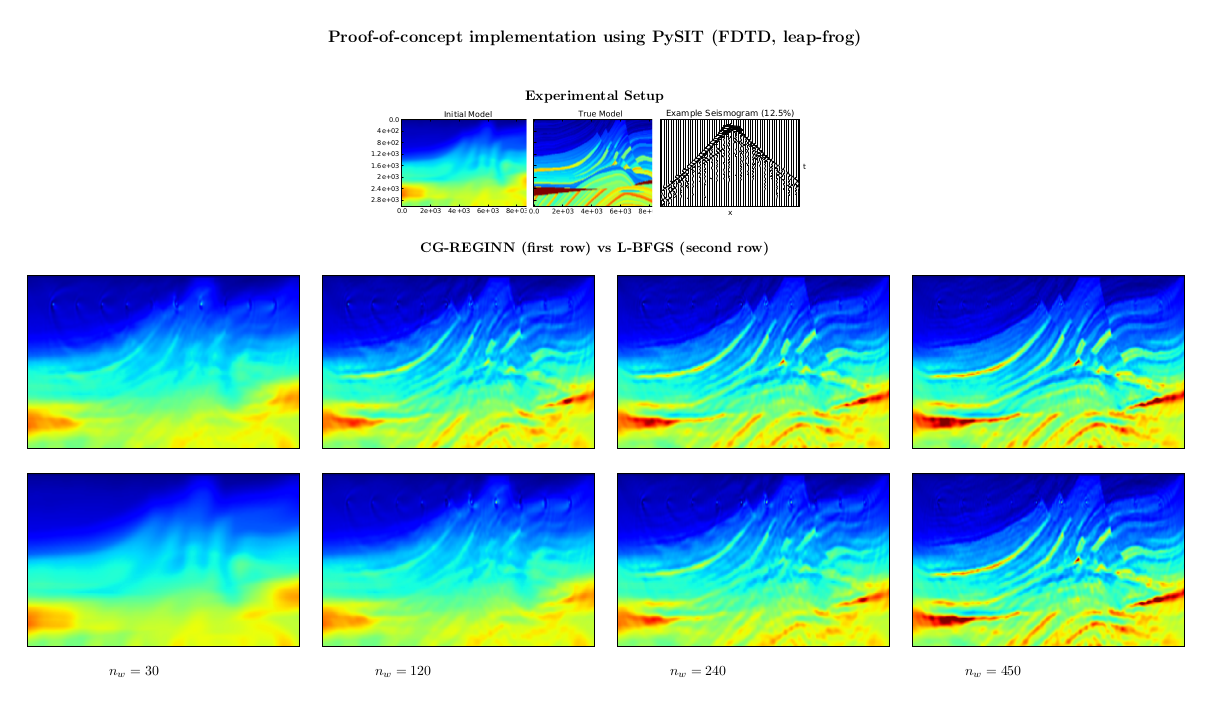
Publications
. On the mathematical foundation of full waveform inversion in viscoelastic vertically transverse isotropic media. Inverse Problems, 41(5):055009, 21, May 2025. URL https://doi.org/10.1088/1361-6420/adcfc0. [preprint]
. Tangential cone condition for the full waveform forward operator in the viscoelastic regime: the non-local case. SIAM J. Appl. Math., 84(2):412–432, April 2024. URL https://doi.org/10.1137/23M1551845. [preprint]
. Multiparameter 2-D viscoelastic full-waveform inversion of Rayleigh waves: a field experiment at Krauthausen test site. Geophys. J. Int., 234(1):297–312, July 2023. URL https://doi.org/10.1093/gji/ggad072. [preprint]
. On the iterative regularization of non-linear illposed problems in $L^{\infty}$. Numer. Math., 154:209–247, June 2023. URL https://doi.org/10.1007/s00211-022-01359-7. [preprint] [files]
. Multiparameter viscoelastic full-waveform inversion of shallow-seismic surface waves with a pre-conditioned truncated Newton method. Geophys. J. Int., 227(3):2044–2057, December 2021. URL https://doi.org/10.1093/gji/ggab311. [preprint]
. Visco-acoustic full waveform inversion: From a DG forward solver to a Newton-CG inverse solver. Comput. Math. Appl., 100:126–140, October 2021. URL https://doi.org/10.1016/j.camwa.2021.09.001. [preprint]
. Tangential cone condition and Lipschitz stability for the full waveform forward operator in the acoustic regime. Inverse Problems, 37(8):085011, 17, July 2021. URL https://doi.org/10.1088/1361-6420/ac11c5. [preprint]
. An all-at-once approach to full waveform seismic inversion in the viscoelastic regime. Math. Methods Appl. Sci., 44(8):6377–6388, May 2021. URL https://doi.org/10.1002/mma.7190. [preprint]
. Random objective waveform inversion of surface waves. Geophysics, 85(4):1JA–Z18, July 2020. URL https://doi.org/10.1190/GEO2019-0613.1.
. 2D multiparameter viscoelastic shallow-seismic full-waveform inversion: reconstruction tests and first field-data application. Geophys. J. Int., 222(1):560–571, July 2020. URL https://doi.org/10.1093/gji/ggaa198. [preprint]
. Inverse problems for abstract evolution equations II: Higher order differentiability for viscoelasticity. SIAM J. Appl. Math., 79(6):2639–2662, December 2019. URL https://doi.org/10.1137/19M1269403. See corrigendum. [preprint]
. High-resolution characterization of near-surface structures by surface-wave inversions: From dispersion curve to full waveform. Surv. Geophys., 40(2):167–195, March 2019. URL https://doi.org/10.1007/s10712-019-09508-0. [preprint]
. Comparison of acoustic and elastic full-waveform inversion of 2D towed-streamer data in the presence of salt. Geophys. Prospect., 67(2):349–361, February 2019. URL https://doi.org/10.1111/1365-2478.12728.
. Individual and joint 2D elastic full-waveform inversion of Rayleigh and Love waves. Geophys. J. Int., 216(1):350–364, January 2019. URL https://doi.org/10.1093/gji/ggy432.
. Estimating S-wave velocities from 3D 9-component shallow seismic data using local Rayleigh-wave dispersion curves – A field study. J. Appl. Geophys., 159:532–539, December 2018. URL https://doi.org/10.1016/j.jappgeo.2018.09.037.
. Inverse problems for abstract evolution equations with applications in electrodynamics and elasticity. Inverse Problems, 32(8):085001, 24, June 2016. URL https://doi.org/10.1088/0266-5611/32/8/085001. [preprint]
. Three-dimensional viscoelastic time-domain finite-difference seismic modelling using the staggered Adams–Bashforth time integrator. Geophys. J. Int., 204(3):1781–1788, March 2016. URL https://doi.org/10.1093/gji/ggv546.
Preprints
. An all-at-once solver for visco-acoustic full waveform inversion in the time-domain. CRC 1173 Preprint 2025/31, Karlsruhe Institute of Technology, July 2025. [files]
. Inexact Newton regularizations with uniformly convex stability terms: a unified convergence analysis. CRC 1173 Preprint 2023/12, Karlsruhe Institute of Technology, April 2023. Revised version of April 2025.
Theses
. All-at-once and reduced solvers for visco-acoustic full waveform inversion. PhD thesis, Karlsruhe Institute of Technology (KIT), November 2023.
. Challenges in near-surface seismic full-waveform inversion of field data. PhD thesis, Karlsruhe Institute of Technology (KIT), November 2020.
. The viscoelastic seismic model: existence, uniqueness and differentiability with respect to parameters. PhD thesis, Karlsruhe Institute of Technology (KIT), December 2018.
. Space-time methods for acoustic waves with applications to full waveform inversion. PhD thesis, Karlsruhe Institute of Technology (KIT), December 2017.
Other references
. A space-time discontinuousa Petrov–Galerkin method for acoustic waves. In U. Langer and O. Steinbach, editors, Space-Time Methods: Applications to Partial Differential Equations, volume 25 of Radon Series on Computational and Applied Mathematics, chapter 3, pages 89–116. De Gruyter, Berlin/Boston, September 2019. [preprint]
. Parallel adaptive discontinuous Galerkin discretizations in space and time for linear elastic and acoustic waves. In U. Langer and O. Steinbach, editors, Space-Time Methods: Applications to Partial Differential Equations, volume 25 of Radon Series on Computational and Applied Mathematics, chapter 2, pages 61–88. De Gruyter, Berlin/Boston, September 2019. [preprint]