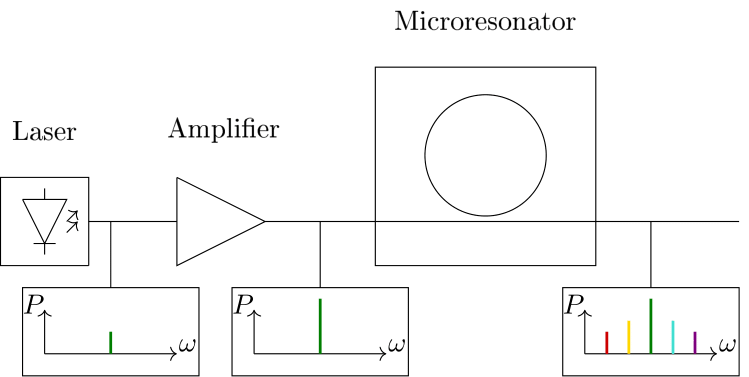
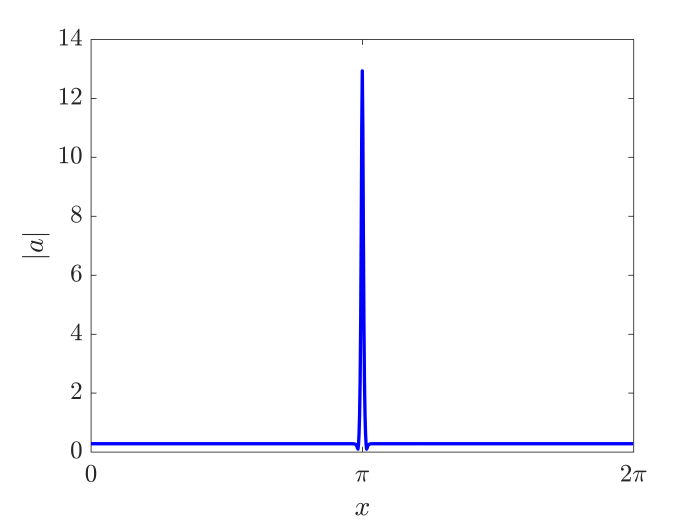
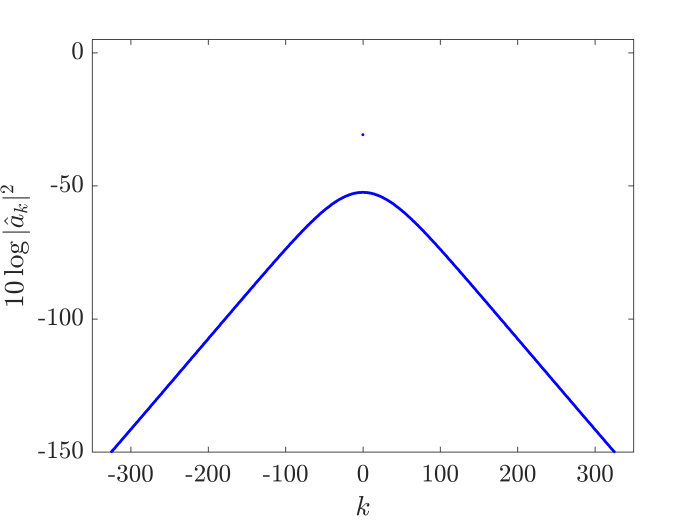
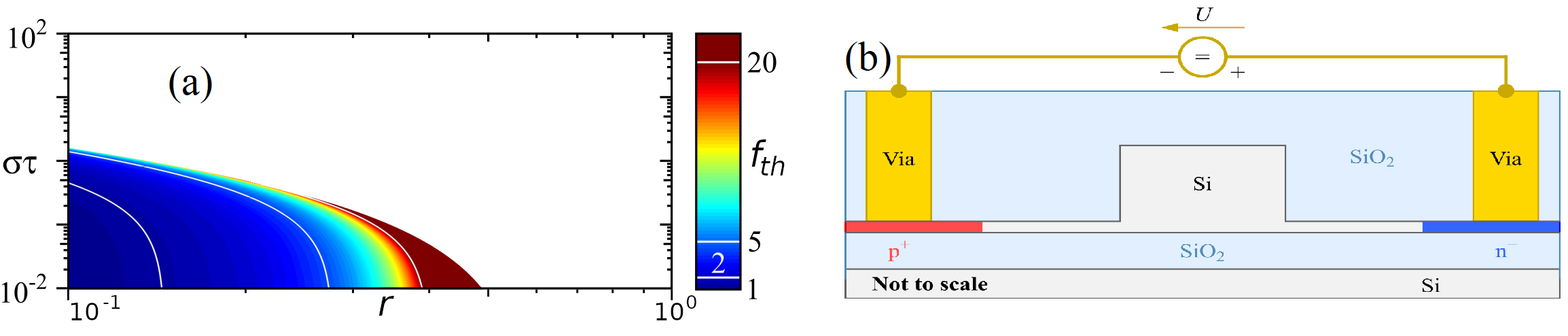
Publications
. Nonlinear dynamics of periodic Lugiato–Lefever waves against sums of co-periodic and localized perturbations. Phys. D, 488:135079, April 2026. URL https://doi.org/10.1016/j.physd.2025.135079. Online first. [preprint]
. Analysis of Kerr frequency combs in microresonators with two-photon absorption and free-carriers. In A. Ott, W. Reichel, and J. A. Warwicker, editors, Applications of Mathematics in Sciences, Engineering, and Economics, Springer Proceedings in Mathematics & Statistics. MathSEE Symposium 2023, pages 221–241, January 2026. Springer, Cham. Online first. [preprint] [files]
. Existence and stability of soliton-based frequency combs in the Lugiato–Lefever equation. Phys. D, 483:134922, December 2025. URL https://doi.org/10.1016/j.physd.2025.134922. [preprint] [files]
. Nonlinear subharmonic dynamics of spectrally stable Lugiato–Lefever periodic waves. Comm. Math. Phys., 405(10):227, 31, October 2024. URL https://doi.org/10.1007/s00220-024-05104-5. [preprint]
. Pinning in the extended Lugiato–Lefever equation. SIAM J. Math. Anal., 56(3):3679–3702, June 2024. URL https://doi.org/10.1137/23M1550700. [preprint] [files]
. Stability of solitary wave solutions in the Lugiato–Lefever equation. Z. Angew. Math. Phys., 75:130, 19pp., June 2024. URL https://doi.org/10.1007/s00033-024-02273-0. [preprint]
. Bandwidth and conversion-efficiency analysis of Kerr soliton combs in dual-pumped resonators with anomalous dispersion. Phys. Rev. A, 108(2):023505, August 2023. URL https://doi.org/10.1103/PhysRevA.108.023505. [preprint]
. Global continua of solutions to the Lugiato–Lefever model for frequency combs obtained by two-mode pumping. Z. Angew. Math. Phys., 74:168, 31pp., July 2023. URL https://doi.org/10.1007/s00033-023-02060-3. [preprint] [files]
. The Lugiato–Lefever equation with nonlinear damping caused by two photon absorption. J. Dyn. Diff. Equat., 34(3):2201–2227, September 2022. URL https://doi.org/10.1007/s10884-021-09943-x. [preprint]
. Soliton solutions for the Lugiato–Lefever equation by analytical and numerical continuation methods. In W. Dörfler, M. Hochbruck, D. Hundertmark, W. Reichel, A. Rieder, R. Schnaubelt, and B. Schörkhuber, editors, Mathematics of Wave Phenomena, Trends in Mathematics, pages 179–195, October 2020. Birkhäuser Basel.
. Performance of chip-scale optical frequency comb generators in coherent WDM communications. Opt. Express, 28(9):12897–12910, April 2020. URL https://doi.org/10.1364/OE.380413.
. Bandwidth and conversion efficiency analysis of dissipative Kerr soliton frequency combs based on bifurcation theory. Phys. Rev. A, 100(3):033819, September 2019. URL https://doi.org/10.1103/PhysRevA.100.033819. [preprint]
. Global secondary bifurcation, symmetry breaking and period-doubling. Topol. Methods Nonlinear Anal., 53(2):779–800, June 2019. URL https://doi.org/10.12775/TMNA.2019.025. [preprint]
. Ultrafast optical ranging using microresonator soliton frequency combs. Science, 359(6378):887–891, February 2018. URL https://doi.org/10.1126/science.aao3924.
. Strang splitting for a semilinear Schrödinger equation with damping and forcing. J. Math. Anal. Appl., 455(2):1051–1071, November 2017. URL https://doi.org/10.1016/j.jmaa.2017.06.004. [preprint]
. Microresonator-based solitons for massively parallel coherent optical communications. Nature, 546:274–279, June 2017. URL https://doi.org/10.1038/nature22387.
. Ultrafast dual-comb distance metrology using dissipative Kerr solitons. In Conference on Lasers and Electro-Optics, STh4L.6, May 2017. Optical Society of America.
. A priori bounds and global bifurcation results for frequency combs modeled by the Lugiato-Lefever equation. SIAM J. Appl. Math., 77(1):315–345, February 2017. URL https://doi.org/10.1137/16M1066221. [preprint]
. 34.6 Tbit/s WDM transmission using soliton Kerr frequency combs as optical source and local oscillator. In European Conference on Optical Communication (ECOC), pages 415–417, December 2016.
. 50 Tbit/s massively parallel WDM transmission in C and L band using interleaved cavity-soliton Kerr combs. In Conference on Lasers and Electro-Optics, STu1G.1, June 2016. [preprint]
Preprints
. Second-harmonic bichromatic dispersive wave comb generation in a dissipative Kerr temporal soliton Fabry-Perot. CRC 1173 Preprint 2025/55, Karlsruhe Institute of Technology, December 2025.
. Multiple front and pulse solutions in spatially periodic systems. CRC 1173 Preprint 2025/5, Karlsruhe Institute of Technology, February 2025. [files]
. Sub-kHz-linewidth external-cavity laser (ECL) with Si${}_3$N${}_4$ resonator used as a tunable pump for a Kerr frequency comb. Preprint, Karlsruhe Institute of Technology (KIT), November 2022.
. Stochastic Galerkin-collocation splitting for PDEs with random parameters. CRC 1173 Preprint 2018/28, Karlsruhe Institute of Technology, October 2018.
Theses
. On the existence and stability of nonlinear waves in Lugiato–Lefever models and in systems with periodic coefficients. PhD thesis, Karlsruhe Institute of Technology (KIT), October 2025.
. On the Lugiato–Lefever model for frequency combs in a dual-pumped ring resonator with an appendix on band structures for periodic fractional Schrödinger operators. PhD thesis, Karlsruhe Institute of Technology (KIT), November 2022.
. Chip-scale optical frequency comb sources for terabit communications. PhD thesis, Karlsruhe Institute of Technology (KIT), February 2021.
. Kerr-nonlinear microresonators and frequency combs: modelling, design and applications. PhD thesis, Karlsruhe Institute of Technology (KIT), November 2020.
. Continuation and bifurcation of frequency combs modeled by the Lugiato–Lefever equation. PhD thesis, Karlsruhe Institute of Technology (KIT), February 2019.
. Terabit-rate transmission using optical frequency comb sources. PhD thesis, Karlsruhe Institute of Technology (KIT), July 2016.
Other references
. Slice-less optical arbitrary waveform measurement (OAWM) in a bandwidth of more than 600 GHz. In 2022 Optical Fiber Communications Conference and Exhibition (OFC), pages 1–3, March 2022.
. Optical arbitrary waveform measurement (OAWM) using silicon photonic slicing filters. J. Light. Technol., 40(6):1705–1717, March 2022. URL https://doi.org/10.1109/JLT.2021.3130764.
. 320 GHz analog-to-digital converter exploiting Kerr soliton combs and photonic-electronic spectral stitching. In 2021 European Conference on Optical Communication (ECOC), pages 1–4, September 2021.