Project B7 • Dynamics of electro-cardiac depolarization waves

Principal investigators

Project summary

Depolarization waves in the heart are an important electrophysiological phenomenon, which is described by the basic model for the cardiac reaction-diffusion system: the bidomain equations for electrical potentials in and between cells and the spread of the depolarization waves. The cardiac electrophysiological system triggers contractions of the heart muscle, which is modeled as a time-varying elastic body. The electrical cellular transmembrane voltages are given as solutions to nonlinear reaction-diffusion equations on a manifold. Depending on the accuracy of the model, this is coupled with an ODE model in every nodal point of every cell to determine the transmembrane currents.

Mathematical model of the heart

Let $\Omega$ be a bounded domain that defines the anatomical regions of the heart and $\Omega_\mathrm{E} \subset \Omega$ be the subset of excitable tissue. Find the transmembrane voltage $v$, the vector of gating variables $\mathbf{w}$, the state variables of the active stress model $\mathbf{s}$, the displacement $\mathbf{u}$, and the state variables of the circulatory system model $\mathbf{z}$, such that our multi scale model of the heart [Ger21] is solved.

$J = \det \mathbf{F} \approx 1$, $\mathbf{D}$ is the diffusion tensor, $C_\mathrm{m}$ is the membrane capacitance, $I_\mathrm{ion}$ is the ionic current, $I_\mathrm{ext}$ is an external stimulus current, $\rho$ is the mass density, $\mathbf{S}$ is the passive stress, $\mathbf{S}_\mathrm{a}$ is the active stress, and $p(t)$ is the blood pressure within the heart chambers. The functions $\mathbf{G_w}, \mathbf{G_s},$ and $\mathbf{G_z}$ are derived from suitable cellular and circulatory system models.

Efficient time integration for the fully coupled model

In [Lin22], different staggered time stepping schemes for the electrophysiology are evaluated systematically. By an asymptotic evaluation for a benchmark configuration (monodomain model with Beeler-Reuter cell model), we show that singular and linear implicit methods for the electric potential with $\mathrm L_2$ projections of the ODE variables are more efficient than operator splitting schemes and simple Lagrange interpolation used up to now.

Electromechanical interaction in health and disease

Hypertrophic cardiomyopathy is a clinically frequently observed disease. However, the underlying disease mechanisms are incompletely understood and alteration of various tissue properties are discussed as being causative. In [Kov21], we could show how the variability in each of these properties contributes to altered mechanics of the left ventricle and which of the alterations is essential to reproduce the phenotype observed in clinical measurements. Similarly, we investigated changes in the electro-mechanical interaction in cases of dilated cardiomyopathy. The characteristic enlargement of the ventricles and the atria leads to a remodeling of the muscle fibers and changes cardiomyocytes on a microscopic level. Which of these pathomechanisms has the most significant impact is studied in [Ger23].

Atrial fibrillation is the most frequent cardiac arrhythmia and ablation therapy is the method of choice for many patients. However, ablation scars alter the electrophysiological activation and the mechanical behavior of the affected atria. In [Ger23], we study five commonly used ablation scar patterns and their combinations in the left atrium regarding their impact on the pumping function of the heart using our electro-mechanical whole-heart model. This study provides biomechanical evidence that atrial ablation has acute effects not only on atrial contraction but also on ventricular pumping function.

Globally, heart failure is a major public health concern affecting 23 million people and causing significant morbidity and mortality. Despite intensive multidisciplinary disease management, the clinical outcomes and prognosis remain unsatisfactory in this population. In [Ger22b], we offer a step-by-step methodological workflow for the in silico analysis of left ventricular rotational behavior using in vivo data obtained during invasive electromechanical mapping in patients with heart failure and co-existing left bundle branch block. We could show that dyssynchronous electrical activation of the left ventricle is insufficient for the breakdown of wringing rotation.

Characterization of cellular pacemaking

The human sinoatrial node (SAN) is the intrinsic natural pacemaker of the heart. Despite its remarkable robustness to failure, the electrophysiological properties, and mechanisms by which the SAN overcomes the source-sink mismatch towards the hyperpolarized surrounding cardiac tissue remains a mystery. The SAN is electrically isolated from the hyperpolarized cardiac tissue, except at a discrete number of sinoatrial exit pathways (SEP). Using in silico experiments, we explore the influence of the fiber orientation, the SEPs’ number, geometry and location on the activation of the SAN and the surrounding atrial tissue. We provide the mechanisms in a first 3D model of the human SAN-SEP structure that can successfully drive the working myocardium [Ams22].

Publications

1. T. Gerach and A. Loewe. Differential effects of mechano-electric feedback mechanisms on whole-heart activation, repolarization, and tension. J. Physiol., 20pp., January 2024. URL https://doi.org/10.1113/JP285022. Online first. [files] [bibtex]

2. J. Fröhlich, T. Gerach, J. Krauß, A. Loewe, L. Stengl, and C. Wieners. Numerical evaluation of elasto-mechanical and visco-elastic electro-mechanical models of the human heart. GAMM-Mitt., 46(3-4):e202370010, September 2023. URL https://doi.org/10.1002/gamm.202370010. [bibtex]

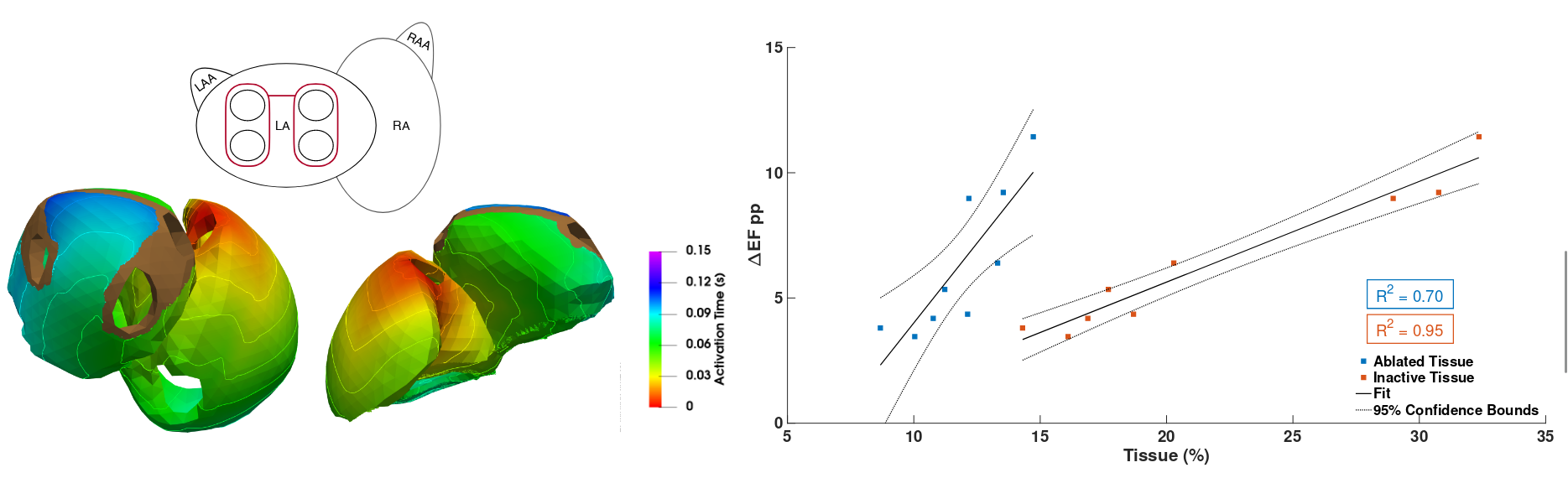
3. T. Gerach, S. Schuler, A. Wachter, and A. Loewe. The impact of standard ablation strategies for atrial fibrillation on cardiovascular performance in a four-chamber heart model. Cardiovasc. Eng. Technol., 14(2):296–314, April 2023. URL https://doi.org/10.1007/s13239-022-00651-1. [preprint] [bibtex]

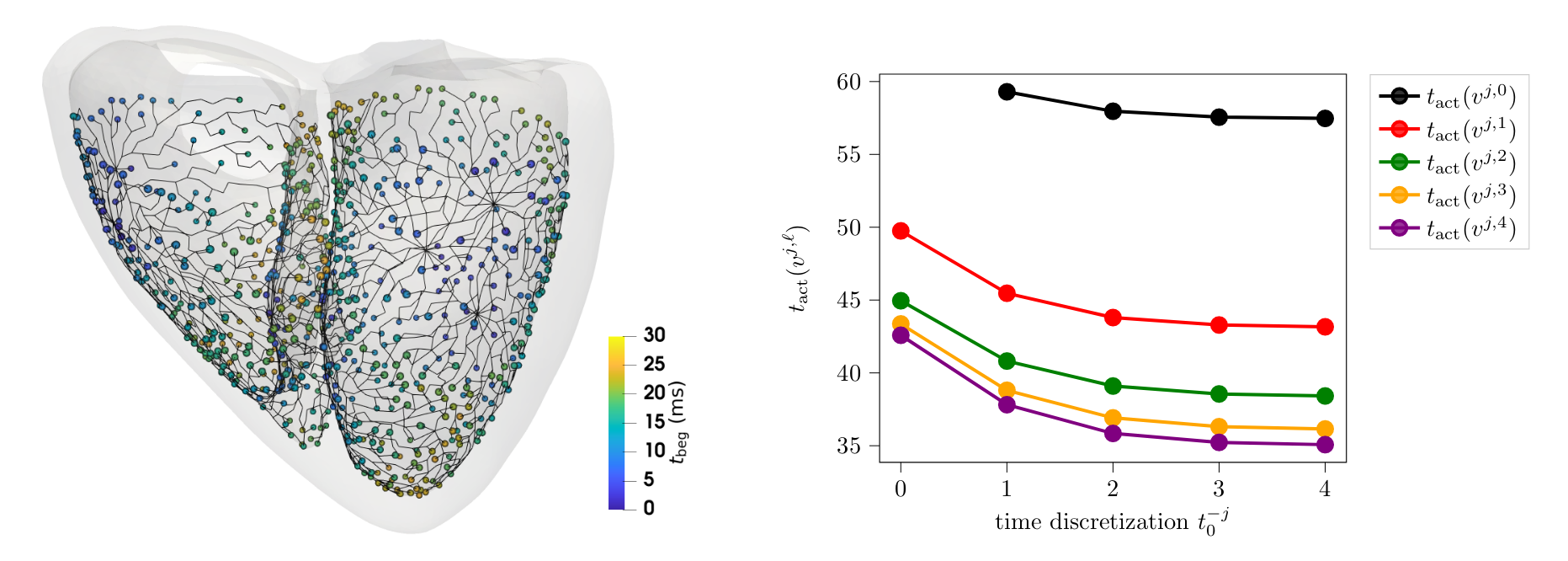
4. L. P. Lindner, T. Gerach, T. Jahnke, A. Loewe, D. Weiss, and C. Wieners. Efficient time splitting schemes for the monodomain equation in cardiac electrophysiology. Int. J. Numer. Method. Biomed. Engng., 39(2):e3666, February 2023. URL https://doi.org/10.1002/cnm.3666. [preprint] [bibtex]

5. N. Tóth, A. Loewe, J. Szlovák, Z. Kohajdam, G. Bitay, J. Levijoki, J. G. Papp, A. Varró, and N. Nagy. The reverse mode of the Na$^+$/Ca$^{2+}$ exchanger contributes to the pacemaker mechanism in rabbit sinus node cells. Sci. Rep., 12(1):21830, December 2022. URL https://doi.org/10.1038/s41598-022-25574-8. [bibtex]

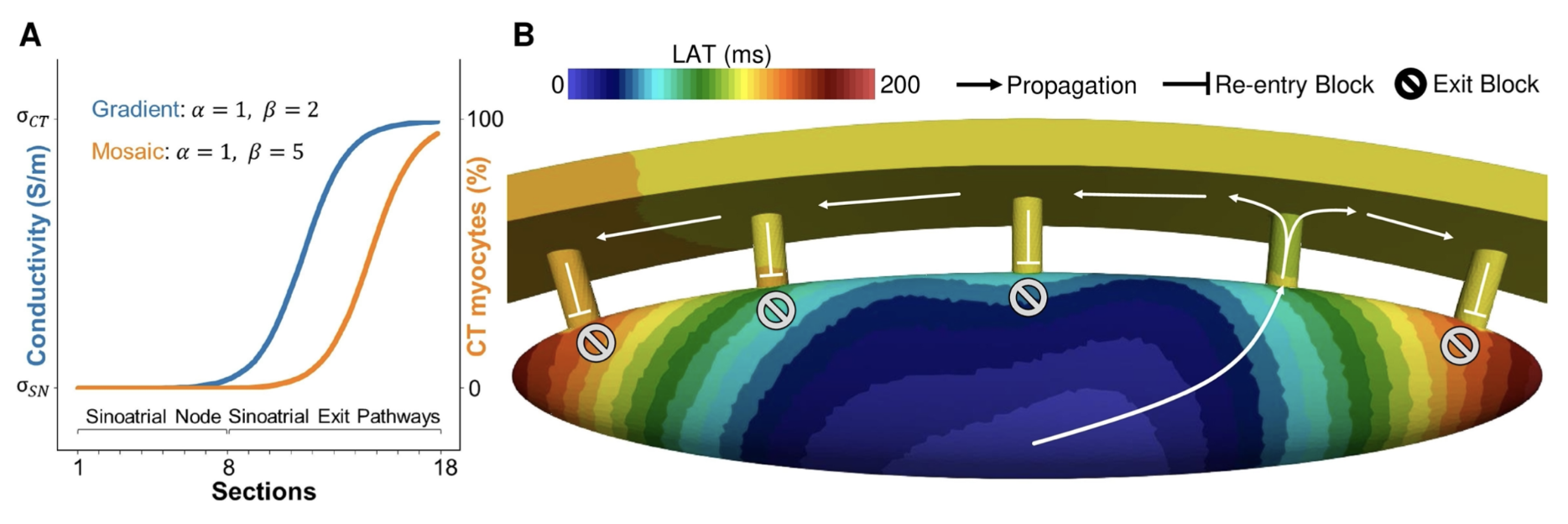
6. A. Amsaleg, J. Sánchez, R. Mikut, and A. Loewe. Characterization of the pace-and-drive capacity of the human sinoatrial node: a 3D in silico study. Biophys. J., 121(22):4247–4259, November 2022. URL https://doi.org/10.1016/j.bpj.2022.10.020. [files] [bibtex]

7. T. Gerach, S. Appel, J. Wilczek, K. Golba, T. Jadczyk, and A. Loewe. Dyssynchronous left ventricular activation is insufficient for the breakdown of wringing rotation. Front. Physiol., 13:838038, May 2022. URL https://doi.org/10.3389/fphar.2022.838038. [bibtex]

8. E. Kovacheva, T. Gerach, S. Schuler, M. Ochs, O. Dössel, and A. Loewe. Causes of altered ventricular mechanics in hypertrophic cardiomyopathy: an in-silico study. BioMed. Eng. OnLine, 20:69, July 2021. URL https://doi.org/10.1186/s12938-021-00900-9. [bibtex]

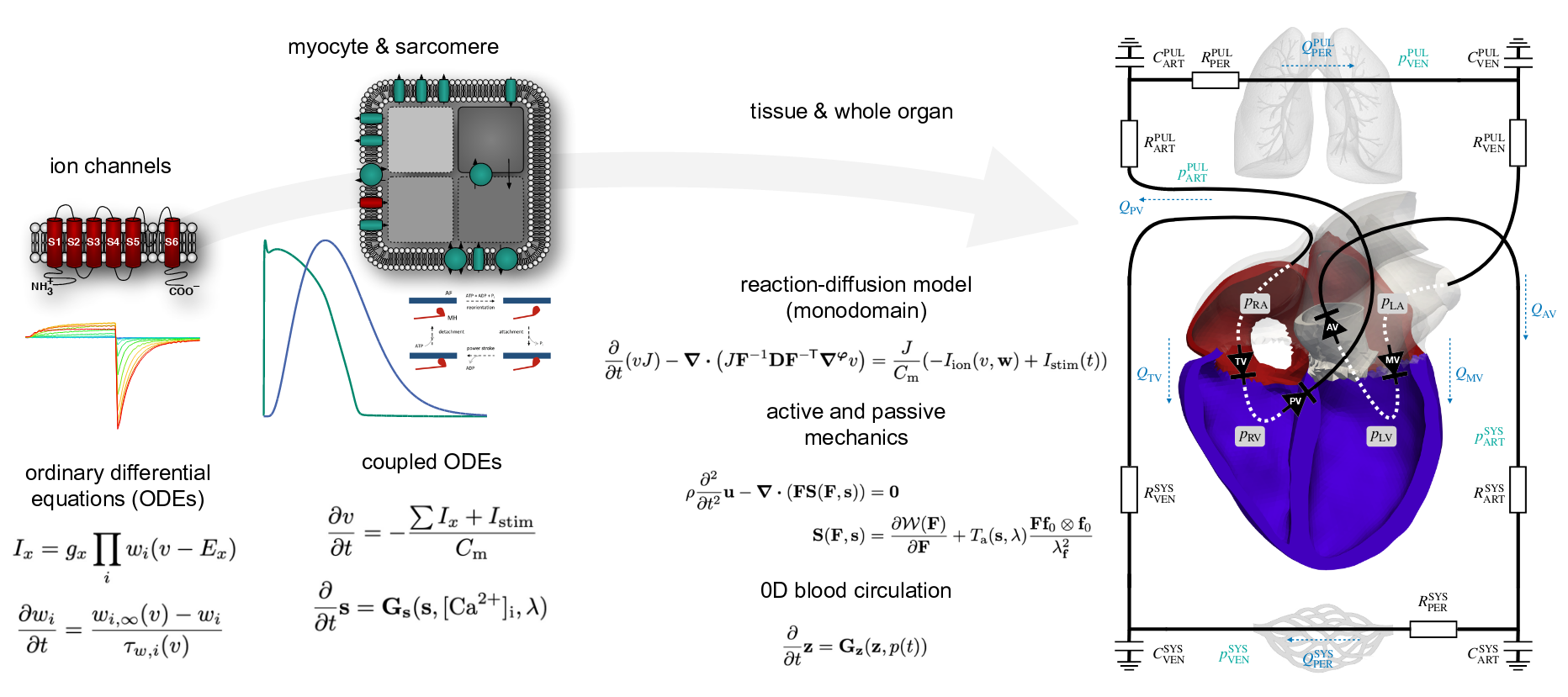
9. T. Gerach, S. Schuler, J. Fröhlich, L. Lindner, E. Kovacheva, R. Moss, E. M. Wülfers, G. Seemann, C. Wieners, and A. Loewe. Electro-mechanical whole-heart digital twins: A fully coupled multi-physics approach. Mathematics, 9(11):1247, May 2021. URL https://doi.org/10.3390/math9111247. [bibtex]

10. L. A. Unger, L. Azzolin, M. Nothstein, J. Sánchez, A. Luik, G. Seemann, S. Yeshwant, T. G. Oesterlein, O. Dössel, C. Schmitt, P. Spector, and A. Loewe. Cycle length statistics during human atrial fibrillation reveal refractory properties of the underlying substrate – a combined in silico and clinical test of concept study. EP Europace, 23(Supplement_1):i133–i142, March 2021. URL https://doi.org/10.1093/europace/euaa404. [bibtex]

11. T. Gerach, S. Schuler, E. Kovacheva, O. Dössel, and A. Loewe. Consequences of using an orthotropic stress tensor for left ventricular systole. In 2020 Computing in Cardiology (CinC), pages 1–4, Rimini, Italy, September 2020. [bibtex]

12. Z. Kohajda, A. Loewe, N. Tóth, A. Varró, and N. Nagy. The cardiac pacemaker story — Fundamental role of the Na${}^{+}$/Ca${}^{2+}$ exchanger in spontaneous automaticiy. Front. Pharmacol., 11:516, April 2020. URL https://doi.org/10.3389/fphar.2020.00516. [bibtex]

13. D. Frisch, T. G. Oesterlein, L. A. Unger, G. Lenis, R. Wakili, C. Schmitt, A. Luik, O. Dössel, and A. Loewe. Mapping and removing the ventricular far field component in unipolar atrial electrograms. IEEE Trans. Biomed. Eng., 67(10):2905–2915, February 2020. URL https://doi.org/10.1109/TBME.2020.2973471. [bibtex]

14. Z. Kohajda, N. Tóth, J. Szlovák, A. Loewe, G. Bitay, P. Gazdag, J. Prorok, N. Jost, J. Levijoki, P. Pollesello, Papp, J. Gy., A. Varró, and N. Nagy. Novel Na${}^{+}$/Ca${}^{2+}$ exchanger inhibitor ORM-10962 supports coupled function of funny-current and Na${}^{+}$/Ca${}^{2+}$ exchanger in pacemaking of rabbit sinus node tissue. Front. Pharmacol., 10:1632, January 2020. URL https://doi.org/10.3389/fphar.2019.01632. [bibtex]

15. A. Loewe, Y. Lutz, D. Nairn, A. Fabbri, N. Hagy, N. Toth, X. Ye, D. H. Fuertinger, S. Genovesi, P. Kotanko, J. G. Raimann, and S. Severi. Hypocalcemia-induced slowing of human sinus node pacemaking. Biophys. J., 117(12):2244–2254, December 2019. URL https://doi.org/10.1016/j.bpj.2019.07.037. [bibtex]

16. A. Loewe, Y. Lutz, N. Nagy, A. S. C. Fabbri, A. Varro, and S. Severi. Inter-species differences in the response of sinus node cellular pacemaking to changes of extracellular calcium. In 41st Annual International Conference, pages 1875–1878, October 2019. IEEE Engineering in Medicine and Biology Society (EMBC), IEEE. [bibtex]

17. T. Gerach, D. Weiß, O. Dössel, and A. Loewe. Observation guided systematic reduction of a detailed human ventricular cell model. In 2019 Computing in Cardiology (CinC), volume 46, pages 1–4, February 2019. [bibtex]

18. A. Loewe, E. Poremba, T. Oesterlein, A. Luik, C. Schmitt, G. Seemann, and O. Dössel. Patient-specific identification of atrial flutter vulnerability—A computational approach to reveal latent reentry pathways. Front. Physiol., 9:1910, January 2019. URL https://doi.org/10.3389/fphys.2018.01910. [bibtex]

19. R. Andlauer, G. Seemann, L. Baron, O. Dössel, P. Kohl, P. Platonov, and A. Loewe. Influence of left atrial size on P-wave morphology: differential effects of dilation and hypertrophy. EP Europace, 20(suppl_3):iii36–iii44, November 2018. URL https://doi.org/10.1093/europace/euy231. [bibtex]

20. T. G. Oesterlein, A. Loewe, G. Lenis, A. Luik, C. Schmitt, and O. Dössel. Automatic identification of reentry mechanisms and critical sites during atrial tachycardia by analyzing areas of activity. IEEE Trans. Biomed. Eng., 65(10):2334–2344, October 2018. URL https://doi.org/10.1109/TBME.2018.2794321. [bibtex]

21. E. Kovacheva, L. Baron, O. Dössel, and A. Loewe. Electro-mechanical delay in the human heart: A study on a simple geometry. In Computing in Cardiology, volume 45, pages 1–4, September 2018. IEEE. [bibtex]

22. M. Alessandrini, M. Valinoti, L. Unger, T. Oesterlein, O. Dössel, C. Corsi, A. Loewe, and S. Severi. A computational framework to benchmark basket catheter guided ablation in atrial fibrillation. Front. Physiol., 9:1251, September 2018. URL https://doi.org/10.3389/fphys.2018.01251. [bibtex]

23. H. Lehrmann, A. S. Jadidi, J. Minners, J. Chen, B. Müller-Edenborn, R. Weber, O. Dössel, T. Arentz, and A. Loewe. Novel electrocardiographic criteria for real-time assessment of anterior mitral line block: "`V1 Jump"' and "`V1 Delay"'. JACC Clin. Electrophysiol., 4(7):920–932, July 2018. URL https://doi.org/10.1016/j.jacep.2018.03.007. [bibtex]

24. A. Loewe and O. Dössel. Commentary: Virtual in-silico modeling gided catheter ablation predicts effective linear ablation lesion set for longstanding persistent atrial fibrillation: Multicenter prospective randomized study. Front. Physiol., 8:1113, December 2017. URL https://doi.org/10.3389/fphys.2017.01113. [bibtex]

25. A. Loewe, M. Wilhelms, J. Schmid, M. J. Krause, F. Fischer, D. Thomas, E. P. Scholz, O. Dössel, and G. Seemann. Parameter estimation of ion current formulations requires hybrid optimization approach to be both accurate and reliable. Front. Bioeng. Biotechnol., 3:209, January 2016. URL https://doi.org/10.3389/fbioe.2015.00209. [bibtex]

Theses

26. T. Gerach. Personalized electromechanical modeling of the human heart: challenges and opportunities for the simulation of pathophysiological scenarios. PhD thesis, Karlsruhe Institute of Technology (KIT), May 2022. [bibtex]

27. L. Baron. In silico modeling, simulation and optimization of human cardiac motion. PhD thesis, Karlsruhe Institute of Technology (KIT), February 2022. [bibtex]

28. A. Loewe. Simulation of cardiac electrophysiology and biomechanics: from model development to clinical translation. Habilitation thesis, Karlsruhe Institute of Technology (KIT), December 2021. [bibtex]

29. E. Kovacheva. Model based estimation of the elastomechanical properties of the human heart. PhD thesis, Karlsruhe Institute of Technology (KIT), July 2021. [bibtex]

30. J. P. Sánchez Arciniegas. A multiscale in silico study to characterize the atrial electrical activity of patients with atrial fibrillation: a translational study to guide ablation therapy. PhD thesis, Karlsruhe Institute of Technology (KIT), June 2021. [bibtex]

Other references

31. A. Quarteroni, T. Lassila, S. Rossi, and R. Ruiz-Baier. Integrated heart—coupling multiscale and multiphysics models for the simulation of the cardiac function. Comput. Methods Appl. Mech. Engrg., 314:345–407, February 2017. URL https://doi.org/10.1016/j.cma.2016.05.031. [bibtex]

32. A. Loewe, M. W. Krueger, F. Holmqvist, O. Dössel, G. Seemann, and P. G. Platonov. Influence of the earliest right atrial activation site and its proximity to interatrial connections on P-wave morphology. Europace, 18(suppl_4):iv35–iv43, December 2016. URL https://doi.org/10.1093/europace/euw349. [bibtex]

33. S. MacNamara and G. Strang. Operator splitting. In R. Glowinski, S. J. Osher, and W. Yin, editors, Splitting methods in communication, imaging, science, and engineering, pages 95–114. Springer, Cham, December 2016. [bibtex]

34. S. Land, V. Gurev, S. Arens, C. M. Augustin, L. Baron, R. Blake, C. Bradley, S. Castro, A. Crozier, M. Favino, T. E. Fastl, T. Fritz, H. Gao, A. Gizzi, B. E. Griffith, D. E. Hurtado, R. Krause, X. Luo, M. P. Nash, S. Pezzuto, G. Plank, S. Rossi, D. Ruprecht, G. Seemann, N. P. Smith, J. Sundnes, J. J. Rice, N. Trayanova, D. Wang, Z. J. Wang, and S. A. Niederer. Verification of cardiac mechanics software: benchmark problems and solutions for testing active and passive material behaviour. Proc. R. Soc. A, 471(2184):20150641, December 2015. URL https://doi.org/10.1098/rspa.2015.0641. [bibtex]

35. L. Baron, T. S. Fritz, and O. Dössel. Sensitivity study of fiber orientation on stroke volume in the human left ventricle. In Computing in Cardiology, volume 41, pages 1–4, September 2014. IEEE. [bibtex]

36. T. Fritz, C. Wieners, G. Seemann, H. Steen, and O. Dössel. Simulation of the contraction of the ventricles in a human heart model including atria and pericardium. Biomech. Model. Mechanobiol., 13:627–641, June 2014. URL https://doi.org/10.1007/s10237-013-0523-y. [bibtex]

37. A. Loewe, M. Wilhelms, F. Fischer, E. P. Scholz, O. Dössel, and G. Seemann. Arrhythmic potency of human ether-à-go-go-related gene mutations L532P and N588K in a computational model of human atrial myocytes. Europace, 16(3):435–443, March 2014. URL https://doi.org/10.1093/europace/eut375. [bibtex]

38. K. H. W. J. ten Tusscher and A. V. Panfilov. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart. Circ. Physiol., 291(3):H1088–H1100, September 2006. URL https://doi.org/10.1152/ajpheart.00109.2006. [bibtex]