Since 7/2019 this project is funded as project C5.
When studying the scattering of electromagnetic waves, the properties of most materials can be described using linear constitutive relations with a scalar permittivity and permeability; and in most cases the latter is nondispersive and close to unity. However, when considering an artificial material that is composed of many and tightly packed complicated scatterers, much more interesting physical effects might be encountered. A pivotal example is optical activity that requires for its description anisotropic, bianisotropic, or chiral constitutive relations. These properties emerge because of a delicate interplay between the geometry of individual scatterers and the material they are made of.
This project is concerned with chirality of scatteres. A geometric object is called achiral if its image under a reflection by any plane, after a suitable rotation, can be superimposed upon it. The object is called chiral if this is not the case. In scattering theory, the mirror image of a propagating wave will have the opposite helicity or circular polarization. This property can be used to define the chirality of a scatterer by means of its interaction with fields of different helicity: An object is electromagnetically chiral if the information obtained by illuminating the object with fields of a given helicity cannot be reproduced using fields of the opposite helicity.
The questions motivating our research are:
- How can we describe the em-chirality of a scatterer mathematically in such a way that we can also obtain a measure of em-chirality that allows us to order scatterers by their chirality or serves as a basis for designing scatterers of a specific em-chirality?
- How does em-chirality relate to other notions of chirality encountered in the scientific literature? What are examples of scatterers with specific chirality properties?
- What procedures can be used to design a scatterer of maximal measure of em-chirality?
A Mathematical Framework for Electromagnetic Chirality
Central to any discussion of chirality in electromagnetics is the concept of the helicity of an electromagnetic field. The simplest solution to the maxwell system, a plane wave is called circularly polarized, if the real part of the electric field amplitude moves in a circle when moving along the direction of propagation. This corresponds to the plane wave being an eigenfunction of the operator \[\frac{1}{k} \operatorname{curl}\] with eigenvalue +1 or -1. More generally, any eigenfunction of this operator for the eingenvalue +1 or -1 is called a field of helicity +1 or -1, respectively. Examples of such fields can easily be constructed as Herglotz wave pairs \[ \begin{pmatrix} E[A](x)\\ H[A](x) \end{pmatrix} = \int_{\mathbb{S}^2} \begin{pmatrix} A(d) \\ d \times A(d) \end{pmatrix} \mathrm{e}^{\mathrm{i} k \, d \cdot x} \, \mathrm{d} s(d)\,,\qquad A \in L^2_t(\mathbb{S}^2)\,,\] which are a common tool in inverse scattering theory. Such a field has helicity \(\pm 1\) if and only if \(\mathrm{i} \, d \times A(d) = \pm A(d)\).
The definition of electromagnetic chirality (em-chirality) given [FFR16] in physical terms serves as the starting point for our mathematical considerations. A scatterer is called em-achiral if its scattering response to fields of one helicity can be fully obtained by incident fields of the opposite helicity and the image of the scatterer under a certain admissable transformation. Otherwise, the scatterer is calles em-chiral. Admissable transformations will include a reflection of the scatterer by some mirror plane and may involve translations and rotations, but also more complex transformations such as dillations or Lorentz boosts.
In a first step [AHHK18], we restrict the mathematical setting to just one frequency and consider only Herglotz wave pairs as incident fields. In this case, em-chirality can be fully characterized by the far field operator, which maps the amplitude function \(A\) of the Herglotz wave pair to the far field pattern of the scattered field.
As pointed out in [FFR16], the definition of em-chirality naturally leads to a scalar measure of chirality and scatterers which maximize this measure relative to the Frobenius norm of the far field operator turn out to be invisible to incident fields of one helicity. We have also studied the relation of this mathematical definition of em-chirality to definitions of chirality based on geometry alone. Geometrically chiral perfect conductors of penetrable non-absorbing scatterers are shown to be em-achiral in [AHHK18].
An example of a maximally em-chiral scatterer
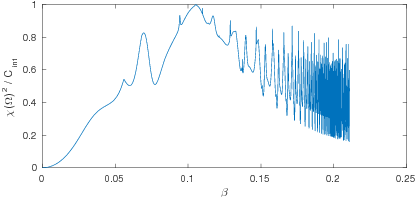
The proposed measure of em-chirality, normalized by the Frobenius norm of the far field operator has a theoretical upper bound of 1. Naturally the question arises, whether this upper bound can actually achieved by some scatterer. This scatterer then has to be invisible to fields of one helicity.
To construct an example of such a scatterer, we considered a specific material law, the Drude-Born-Federov constitutive relations which read as \[ \frac{1}{\sqrt{\varepsilon_0}} D = \varepsilon_r (E + \beta \operatorname{curl}E), \quad \frac{1}{\sqrt{\mu_0}} B = \mu_r (H + \beta \operatorname{curl} H)\,, \] with additional chirality parameter \(\beta\). We considered the case of \(\Omega\) being a ball, surrounded by vacuum with continuous transmission conditions \[ [\nu \times E] = 0, \quad [\nu \times H] = 0 \quad \text{on } \partial \Omega.\] We were able to state an explizit formula for \(\chi(\Omega)\) using expansions of the scattered field into vector spherical harmonics. By this formula, one can see that there exists a critital value of \(\beta\) such that the normalised measure of em-chirality attains the theoretical maximum of \(1\) which can be seen in the figure. Furthermore, one can see, that we can not expect the measure to be smooth. This has to be taken into account for the shape optimisation.