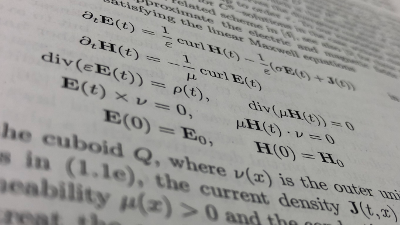Research Program

For CRC scientists working on wave phenomena research focuses on carefully selected topics related to typical wave phenomena. An interdisciplinary approach creates substantial synergy effects, which is necessary to answer fundamental questions and to solve newly emerging challenges in wave phenomena. In particular, the transfer of knowledge between disciplines yields new insights and ultimately lead to a better mathematical understanding of central aspects of wave phenomena. Especially for mathematicians searching on waves, the wave propagation is described by a number of intriguing equations with beautiful properties. Furthermore the holistic point of view which consists in a unified approach of analysis and numerical mathematics, enhanced with an interdisciplinary interface to selected applications in other sciences, will trigger new developments. Our goal is to analytically understand, numerically simulate, and eventually manipulate wave propagation under realistic scenarios by intertwining analysis and numerics.